Computer Security :: Lessons :: Random Numbers
Random Numbers
Random numbers are essential to cryptography. Random numbers can be used for key distribution. Random numbers can be used for the nonce to authenticate communication. Sessions are transactions that are valid for a particular period of time, and are used frequently in web apps. Random numbers can be used as the session key in many situations. Random numbers can also be used for keys in the RSA encryption algorithm and bit streams for symmetric stream encryption.
The two distinct requirements of random numbers are randomness and unpredictability. The criteria to evaluate the randomness of a sequence of numbers is the uniform distribution of the numbers, or the frequency of zeros and ones should be approximately equal, and the independence or the numbers, meaning one number in the sequence will not affect any other numbers in the sequence. The unpredictability of a number means there should not be a way for someone to predict future sequences of the random number generation.
True Random Number Generators
True random numbers generators, or TRNGs, take a source of input that is effectively random, known as the entropy source and convert that source from analog to binary. Sound from a microphone or video from a camera are sometimes used as the entropy source. In addition, traditional hard disk drives have random fluctuations in their rotational speed due to air turbulence. The online service Random.org uses atmospheric noise to generate random numbers for the public. A process to mitigate potential bias in the true random numbers is called deskewing, which modifies a bit stream to reduce or eliminate any bias that has developed.
Pseudorandom Number Generators
Pseudorandom numbers generators, or PRNGs, use an algorithm to generate numbers that appear random. A fixed value, called a seed is input into the algorithm to generate numbers. A pseudorandom function is nearly identical to a pseudorandom number generator, but also takes a context-specific value such as a user ID or application ID in addition to a seed.
Even though a PRNG is deterministic, it is essential that it appear to be random. To validate that a PRNG appears random, it must be uniform so the expected number of zeros or ones is n/2 where n is the length of the sequence, it must be scalable so all subsequences of the larger sequence can be considered random, and it must be consistent across all seeds. A PRNG must also be unpredictable both forward and backward. If the seed is unknown, the next output bit should not be predictable despite any knowledge of previous bits. It should also be impossible to determine the seed from any knowledge of the generated bits.
Generally, the seed for a PRNG is generated by a TRNG. The seed can help an attacker determine the output of the PRNG so true random numbers are necessary. A TRNG cannot always generate enough random numbers to keep up with application requirements, which is why a PRNG may be necessary for many applications. If you are interested in the design of specific algorithms for PRNG check out this video.
Block Cipher PRNGs
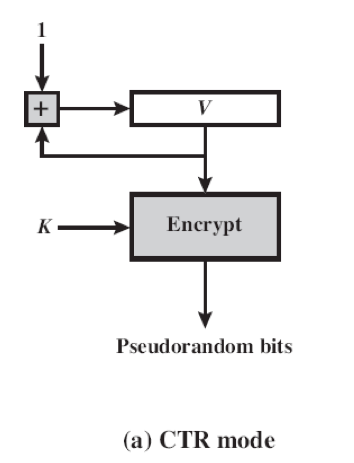
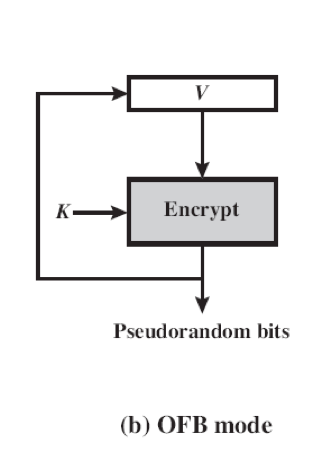
CTR mode and OFB mode are the two recommended block cipher modes of operations for pseudorandom number generation. As an example, AES-128 would use a seed consisting of a 128-bit key and a 128-bit value, referred to as V. In CTR mode, V is increased by 1 after each encryption. In OFB mode, V is updated to equal the preceding PRNG block. Both modes produce one block of output at a time (128 bits in the case of AES-128).
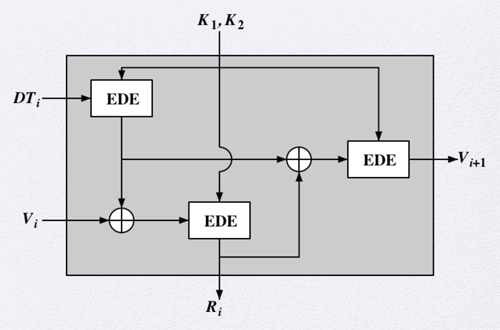
ANSI X9.17 specifies one of the cryptographically strongest PRNGs that is used for financial security applications and PGP. The specification uses 3DES for encryption with two pseudorandom inputs driving the generator. One input is a 64-bit representation of the current date and time, which is updated after each generation. The other input is a 64-bit seed. The same pair of keys is used for each DES operation. The diagram below shows how the ANSI X9.17 specification works where DTi is the date/time value at the beginning of generation stage i, Vi is the seed value at the beginning of generation stage i, Ri is the Pseudorandom number produced by generation stage i, and K1 and K2 are the DES keys.
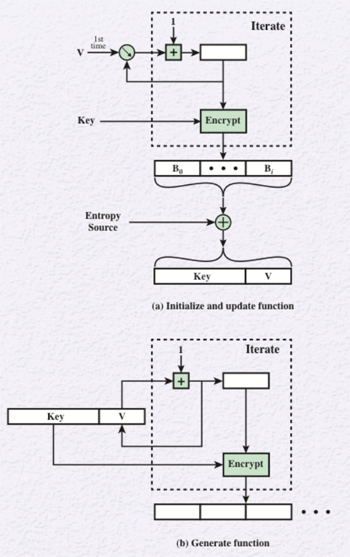
CTR_DRBG is a counter mode-deterministic random bit generator that is widely used for hardware-based random number generation. The DRBG uses an entropy source uses 3DES with three keys or AES. The four parameters for this algorithm are output block length, or outlen, which specifies the length of the output block, key length, or keylen, which specifies the length of the encryption key, seed length, or seedlen, which is outlen + keylen, and the reseed interval, or reseed_interval, which is the maximum number of output blocks generated before updating the seed.
The initialize phase of CTR_DRBG uses the initialize and update function. CTR mode requires an encryption key and an initial counter value (V). The combination of the key and V is the seed for CTR_DRBG. The initial values for the key and V can be chosen arbitrarily. These values must be at least seedlen bits long and the entropy source must supply exactly seedlen bits. The CTR mode is iterated to produce a sequence of output blocks and V is incremented by 1 after each encryption. The leftmost seedlen bits of output are then XORed with the entropy source bits to produce a new seed comprising V and the key. The leftmost keylen bits of the seed form the new key and the rightmost outlen bits of the seed form the new V.
The generate phase of CTR_DRBG is given the values of the key and V from the initialize or update phase. One output block at a time is generated and the encryption function is iterated to generate the number of bits desired. Each iteration uses the same encryption key, but V is incremented by 1 for each iteration.
The update phase of CTR_DRBG uses the reseed_interval to limit the number of bits generated using a single seed. During the generate phase the reseed counter is initialized to 1 and incremented with each iteration. When the reseed counter reaches the reseed interval, the update function is invoked, which is the same as the initialize function. The update function changes both the key and V values used by the generate function.



